Daily Archives: August 30, 2012

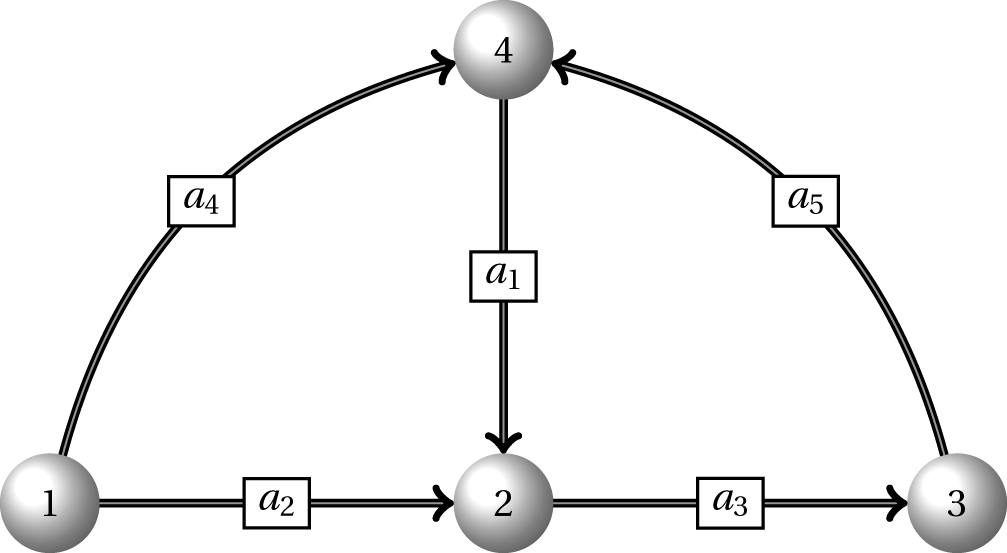
Often when I teach students at our Business School they have a hard time understanding compact linear programming (LP) formulations. So here it is,  a short introduction to some of the concepts you need to know for understanding compact LP formulations. Sets A set is a group of elements, e.g. $\{1,2,4\}$ is a set with 3 elements, namely, $1,2$ and $4$ and $A=\{(2,3),(4,5),(6,8),(5,6)\}$ is a set called $A$ with 4 elements (pairs), namely,  $(2,3),(4,5),(6,8)$ and $(5,6)$. Note that in the last case each element is a pair $(i,j)$. Sets containing pairs are often used when we formulate LPs based on network problems where the pair $(i,j)$ denote the arc/edge from node $i$ to node $j$.